Via Walking Randomly's post Fractals on Wolfram Alpha – an update I stumbled upon his previous post Plotting Fractals with Wolfram Alpha. And something struck me, I invented / discovered those H-trees when I was a little kid! I remember drawing them when I was in second grade (you're 7 years old then, at least in Belgium), enjoying the laborious yet beautiful nature of them. I also drew gigantic heaps of blocks in oblique projection, oh, how many sheets of grid paper (5 by 5 millimetre) I have filled that way... I guess I was the weird kid of our class.

I wanted to board train nostalgia and draw them in TikZ. And this was even easier than I imaged, as there is a library for fractal decorations! If only TikZ did the dishes. Based on the code I found in $TEXMF/tex/generic/pgf/libraries/pgflibrarydecorations.fractals.code.tex I quickly hacked together the following code: 

\pgfdeclaredecoration{H-tree}{init}
{
  \state{init}[width=\pgfdecoratedinputsegmentremainingdistance]
  {
    \pgfpathmoveto{\pgfpoint{0pt}{0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathlineto{\pgfpoint{0pt}{-0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathmoveto{\pgfpoint{0pt}{0pt}}
    \pgfpathlineto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0pt}}
    \pgfpathmoveto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathlineto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{-0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathmoveto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0pt}}
  }
}

This code must be either placed in $TEXMF/tex/generic/pgf/libraries/pgflibrarydecorations.fractals.code.tex or the file itself (or your personal contain-it-all package, just someplace where it can be found).

Now you just draw a tikzpicture with a single recursively decorated line: 

\begin{tikzpicture}[decoration=H-tree]
  \draw decorate{decorate{decorate{decorate{decorate{decorate{ (0,0) -- (5,0) }}}}}};
\end{tikzpicture}
which results in

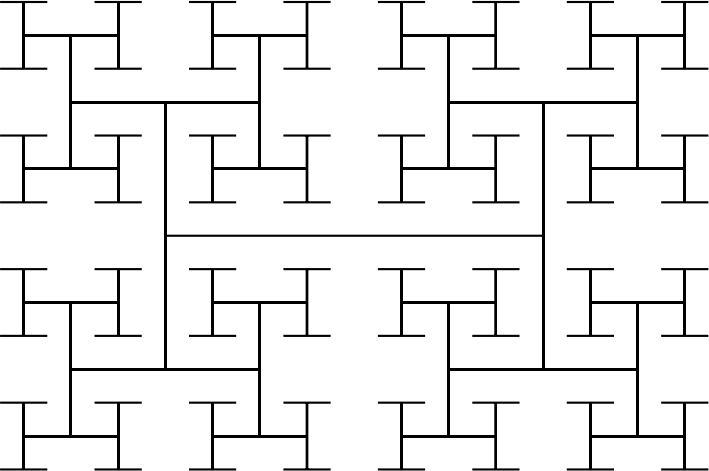
An H-tree, drawn in TikZ

I hope I got the factor right, but I guess 1/(2sqrt(2)) is the one I needed. A complete minimal working example is given: 

\documentclass{minimal}
\usepackage{tikz}
\usetikzlibrary{decorations.fractals}

\pgfdeclaredecoration{H-tree}{init}
{
  \state{init}[width=\pgfdecoratedinputsegmentremainingdistance]
  {
    \pgfpathmoveto{\pgfpoint{0pt}{0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathlineto{\pgfpoint{0pt}{-0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathmoveto{\pgfpoint{0pt}{0pt}}
	\pgfpathlineto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0pt}}
    \pgfpathmoveto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathlineto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{-0.35355\pgfdecoratedinputsegmentremainingdistance}}
    \pgfpathmoveto{\pgfpoint{\pgfdecoratedinputsegmentremainingdistance}{0pt}}
  }
}

\begin{document}
  \begin{tikzpicture}[decoration=H-tree, very thick]
    \draw decorate { decorate { decorate { decorate { decorate { decorate { (0,0) -- (5,0) }}}}}};
  \end{tikzpicture}
\end{document}
which should result in (after pdfcrop) this output. LaTeX easily exceeds its total allocated memory, more iterations are impossible (unless you decrease the length of the line or the zooming factor, for some reason).