Fano varieties are varieties satisfying a positivity criterion. Higher Fano varieties are varieties satisfying a stronger positivity criterion. There is a hierarchy of $k$-Fanoness, with $k=1$ being the usual condition that the anticanonical bundle is ample. For general $k$, one asks that $\mathrm{ch}_i(\mathrm{T}_X)\cdot Z>0$ for all effective codimension-$i$ cycles and all $i=1,\ldots,k$.

For the wonderful properties that $k$-Fano varieties satisfy I refer you to Carolina Araujo, Roya Beheshti, Ana-Maria Castravet, Kelly Jabbusch, Svetlana Makarova, Enrica Mazzon, Libby Taylor, Nivedita Viswanathan: Higher Fano manifolds.

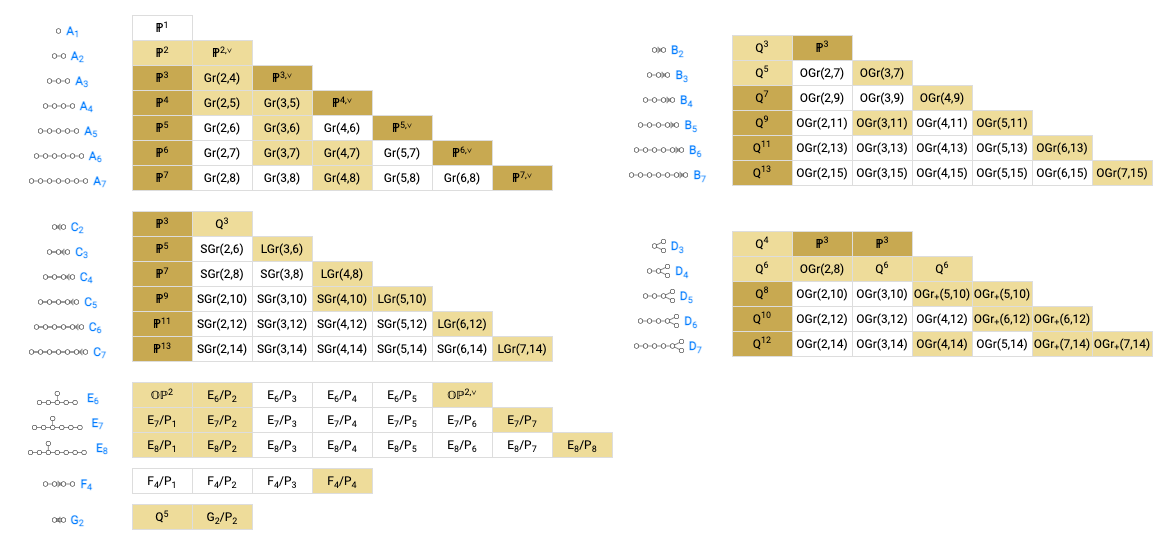
This paper also classifies the generalised Grassmannians for which $k\geq 2$. In those cases $k=2$ except for projective spaces and sufficiently high-dimensional quadrics. So it is a really strong positivity criterion. See Theorem 1.3 for the classification.

This post mostly serves to announce that this information is now also contained in Grassmannian.info, both on the main page and on the detail pages. Thanks to Enrica Mazzon for interesting discussions!