There is another new-ish paper on the arXiv now: Graph potentials and topological quantum field theories.

Last week I announced a new-ish paper which was split off from a large preprint by Sergey Galkin, Swarnava Mukhopadhyay and myself. The new installment is really the first part, in which we define the novel object (namely graph potentials) whose properties we study.


The main goal of this paper is to properly define graph potentials, and study their basic properties. They are Laurent polynomials in $3g-3$ variables, where $g$ refers to the genus of a trivalent graph used to define them. Locally a trivalent graph looks like

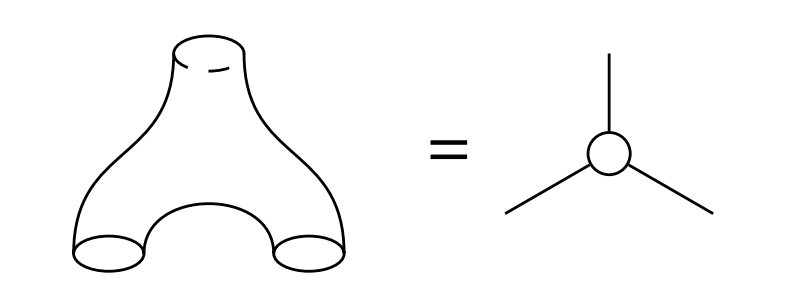
where we also see its topological origin relevant for us, from pair-of-pants decompositions of surfaces.

Labelling the outgoing half-edges as $x,y,z$ and incorporating a coloring $c$ of the vertex (which can be either $0$ or $1$) we can define a Laurent polynomial in $x^{\pm},y^{\pm},z^{\pm}$ as \begin{equation} W= \begin{cases} xyz+\frac{x}{yz}+\frac{y}{xz}+\frac{z}{xy} & c=0 \\ \frac{1}{xyz}+\frac{xy}{z}+\frac{xz}{y}+\frac{yz}{x} & c=1 \end{cases} \end{equation}

For a trivalent graph of genus $g$ without half-edges this defines a Laurent polynomial in $3g-3$ variables, the graph potential. Why is this an interesting object? Topologically speaking, trivalent graphs reflect pair-of-pants decompositions of a surface, and there can be many such decompositions, all related via special operations. For us the main operation is

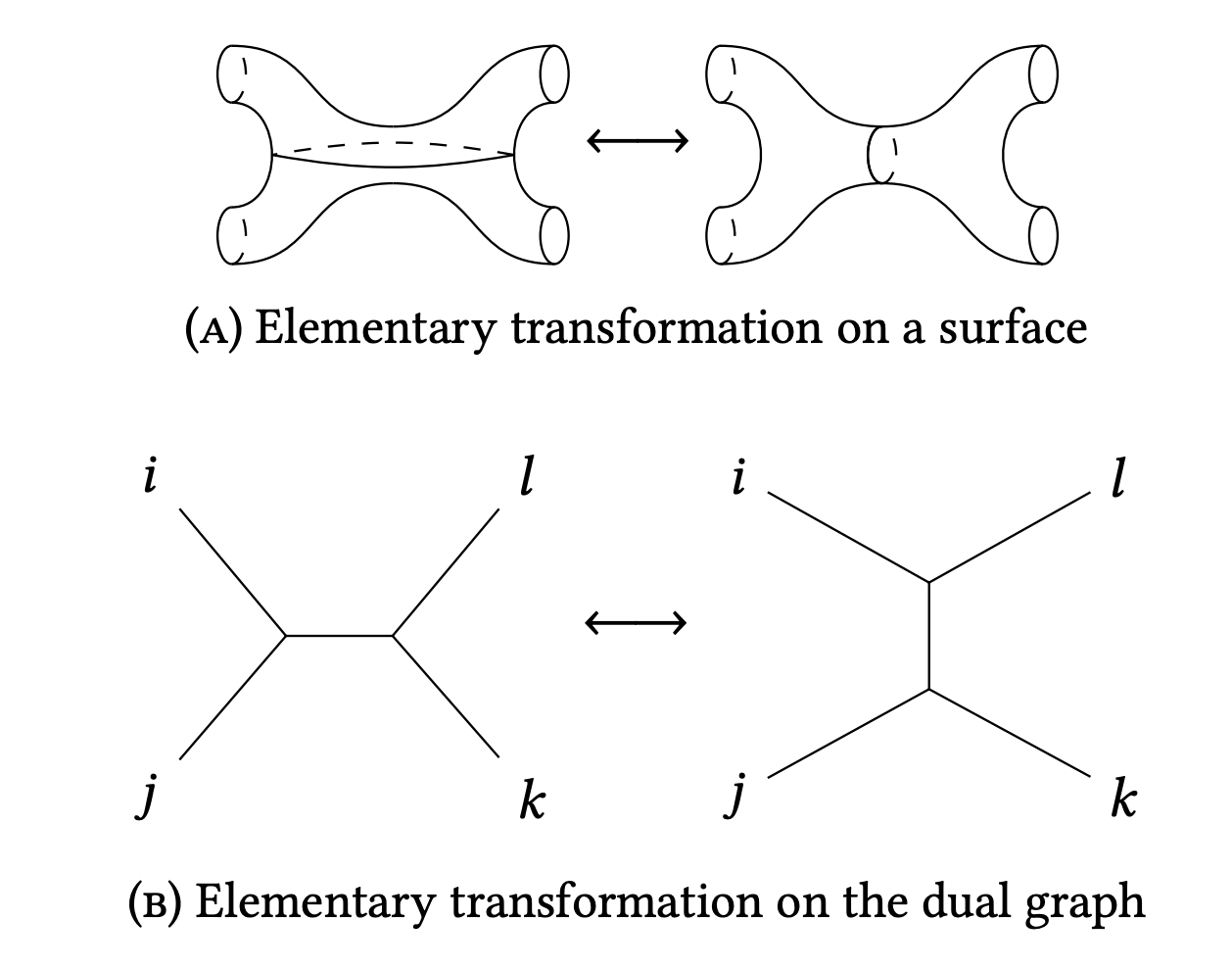
and such an operation induces transformations between the graph potentials. The choice of trivalent graph influences the shape of the Laurent polynomial, but not really its properties! We are mostly interested in its classical period, which for any Laurent polynomial can be defined as (although this doesn't quite reflect its Hodge-theoretical origins very well) \begin{equation} \pi_W(t)=\sum_{k\geq 0}[W^k]_0t^k \end{equation} where $[f]_0$ is the constant term of a Laurent polynomial.

This fact allows us to define a topological quantum field theory which computes its classical period really efficiently. The great thing about this computational approach is that it works for all genera simultaneously, and one can implement this implementation super-easily on a computer.

The paper also surveys what happens in the rest of the series (2 more parts to come, so 4 in total). So if you want to read 5 pages out of the 100+, this paper's introduction is probably your best choice.