In A simple counterexample to the Jordan-Hölder property for derived categories Alexander Kuznetsov discusses a counterexample to the Jordan-Hölder property for a derived category. The Jordan-Hölder property states that any two semiorthogonal decompositions with indecomposable components are necessarily of the same length, and the components in one decomposition are the same as in the other decomposition up to permutation.

The counterexample is based on an algebra introduced by Alexey Bondal (and Alexander Polishchuk), and makes its first appearance in Bondal–Polishchuk, Homological properties of associative algebras: the method of helices, as the algebra $A(2,2,2)$ in example 2.8, where another pathology (non-geometricity) for this algebra is discussed.

In the preprint (I'm not sure whether it's intended for publication) Kuznetsov only gives the definition of the algebra $A=A(2,2,2)$, and defines an $A$-module $P$, which he claims is an exceptional object in the derived category, and suggests that one cannot extend this exceptional object to a full exceptional collection of three objects, but the computations are missing. I decided to have a little fun with this example, fleshing out the details. Recall that the algebra $A$ is defined as

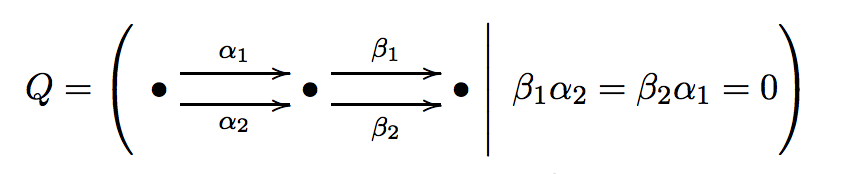
and the module $P$ is

.

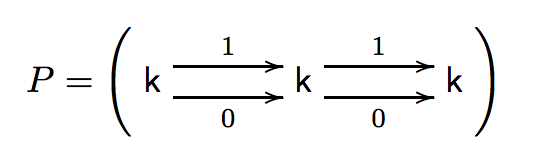Exceptionality For this we need to check that \begin{equation} \operatorname{Ext}_{A}^i(P,P) = \begin{cases} k & i=0 \\ 0 & i\neq 0. \end{cases} \end{equation}

As a nice showcase of what one can do with QPA, here is the code which allows us to check that this is indeed an exceptional object. 

LoadPackage("qpa");

Q := Quiver(3, [[1, 2, "a1"], [1, 2, "a2"], [2, 3, "b1"], [2, 3, "b2"]]);;
kQ := PathAlgebra(Rationals, Q);;
AssignGeneratorVariables(kQ);;

I := [a2*b1, a1*b2];;
A := kQ / I;;

P :=  RightModuleOverPathAlgebra(A, [ ["a1", [[1]]], ["a2", [[0]]],
                                      ["b1", [[1]]], ["b2", [[0]]] ]);;

# it is exceptional
ExtAlgebraGenerators(P, 3);

Beware when defining quotients of path algebras in QPA: do not use the method Ideal before taking the quotient. The quotient construction will return the wrong type of algebra, and all consecutive steps will fail. This caused me some confusion...

The method ExtAlgebraGenerators describes the generators of the Ext-algebra of a module, and we tell QPA that we only need things up to degree 3 (because we know that the global dimension of $A$ is at most 3). The output is

[ [ 1, 0, 0, 0 ], [ 1, 0, 0, 0 ], [ [ <<[ 1, 1, 1 ]> ---> <[ 1, 1, 1 ]>> ], [ ], [ ], [ ] ] ]

The only thing relevant to us right now is the first [ 1, 0, 0, 0 ], which gives us the dimension of $\operatorname{Ext}_A^i(P,P)$, from which we can conclude that it is indeed an exceptional object. I usually don't trust myself with pen and paper computations alone, so I'm glad I have computer algebra backing me up.

In a next post we will continue the discussion of this example, and show that it is not possible to extend this exceptional object to a full exceptional collection;